PID 算法详细介绍
介绍
1.1 概述
比例(Proportion)积分(Integral)微分(Differential)控制器(PID控制器或三项控制器)是一种采用反馈的控制回路机制,广泛应用于工业控制系统和需要连续调制控制的各种其他应用。
PID控制器连续计算误差值 e(t) 作为所需设定点(SP) 和测量过程变量(PV)之间的差值,并应用基于比例、积分和导数项(分别表示为P、I和D)的校正,因此得名。
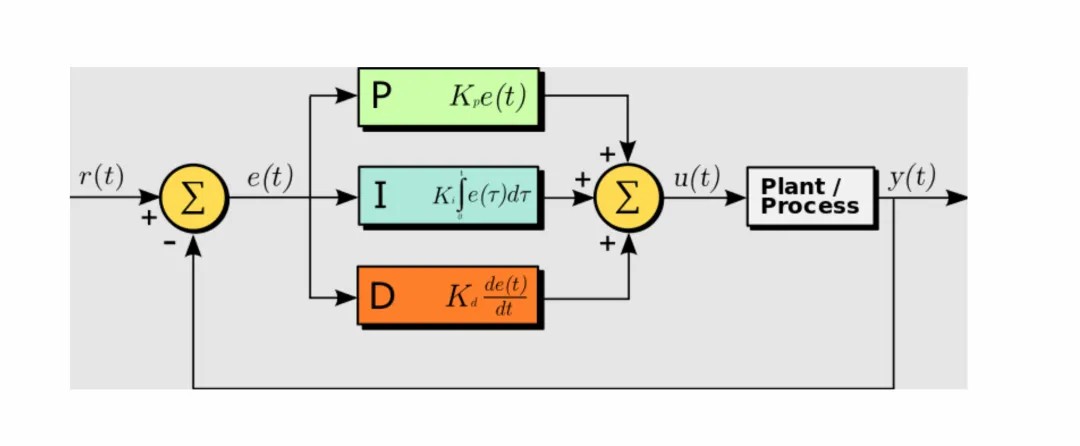
r(t) 是期望的过程值或设定点(SP),y(t) 是测量的过程值(PV)。
1.2 历史发展
1911年,第一个PID控制器是由Elmer Sperry开发的。
1922 年,俄裔美国工程师尼古拉斯·米诺斯基 ( Nicolas Minorsky)才首次利用理论分析制定了我们现在所说的 PID 或三项控制的正式控制律。米诺斯基当时正在为美国海军研究和设计自动船舶转向系统,他的分析基于对舵手的观察。
他指出,舵手不仅根据当前航向误差,还根据过去的误差以及当前的变化率来驾驶船舶;然后 Minorsky 对此进行了数学处理。他的目标是稳定,而不是一般控制,这大大简化了问题。
1933年,TIC(泰勒仪器公司)实现了完全可调节的前气动控制器。几年后,控制工程师通过将末端返回到一些假值,直到误差不为零,消除了比例控制器中发现的稳态误差。这个返回包含了误差,这被称为比例积分控制器。
1940年,第一个气动PID控制器通过导数动作开发,以减少超调问题。
1942年,Ziegler & Nichols引入了调谐规则,由工程师发现和设置PID控制器的合适参数。
20世纪50年代中期,自动PID控制器在工业上得到了广泛的应用。工业中大多数现代 PID 控制都是作为DCS、PLC 或单片机程序来实现的。
1.3 应用
•火箭的姿态控制
•无人机悬停控制等
•相机稳定器、相机云台
•平衡小车
•汽车的定速巡航控制、转向控制
•发动机转速控制
•3D打印机上的温度控制器
•工业自动化领域,大约95%的闭环操作使用PID控制器。
1.4 与 ON/OFF 型控制器对比
像PID控制器这样的闭环系统包括一个反馈控制系统。该系统利用一个固定点对反馈变量进行评估,从而产生误差信号。在此基础上,它改变系统输出。这个过程将继续,直到误差达到零,否则反馈变量的值就等于一个固定点。
与ON/OFF型控制器相比,该控制器提供了良好的效果。在开/关型控制器中,只需两个条件即可管理系统。大多数暖通空调系统、冰箱都采用这种方法。
例如,在冰箱中,它会冷却内部直到达到所需温度,然后关闭冷却器,直到达到高于所需温度的设定值。一旦工艺值低于固定点,则开启。
类似地,一旦该值高于固定值,它将关闭。这种控制器的输出不稳定,在不动点的区域内振荡频繁。然而,与ON/OFF型控制器相比,PID 控制器更加稳定和准确。

1.6 响应类型
Introduction to PID:
https://docs.wpilib.org/en/stable/docs/software/advanced-controls/introduction/introduction-to-pid.html
由PID控制器驱动的系统通常具有三种类型的响应:欠阻尼、过阻尼和临界阻尼。
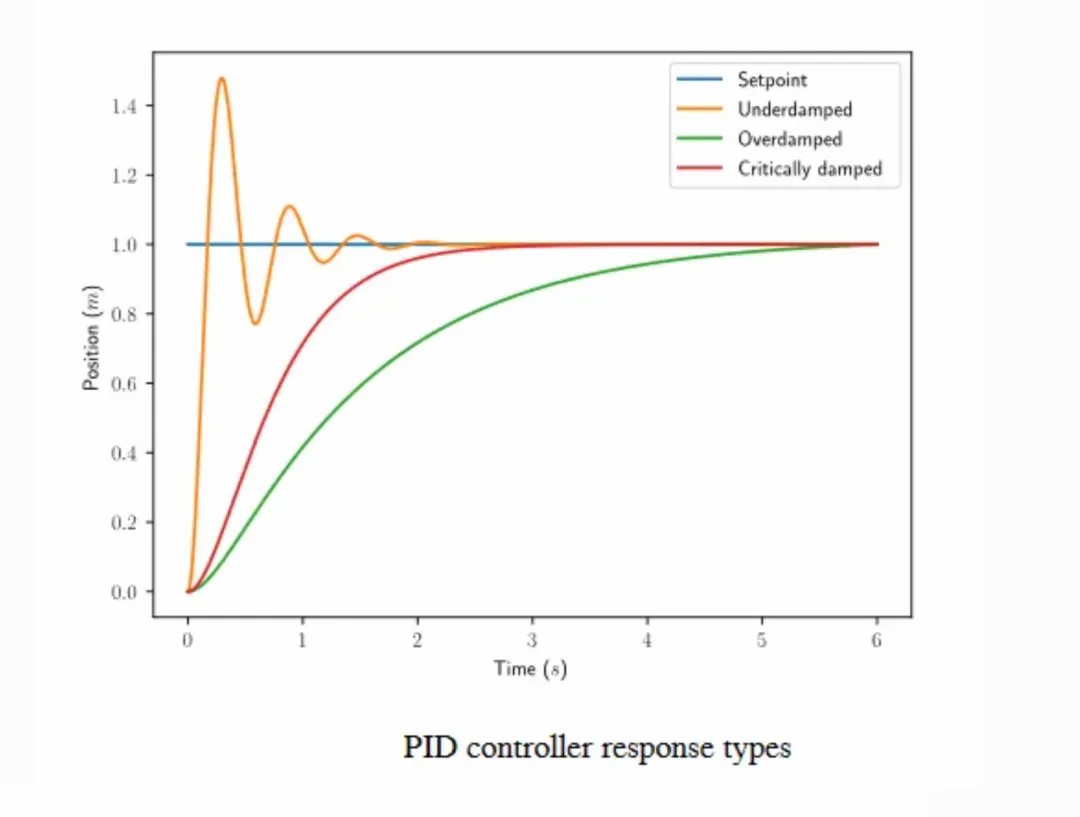
•欠阻尼响应在稳定之前围绕参考值振荡。
•过阻尼响应上升缓慢并且不会超过参考值。
•临界阻尼响应具有最快的上升时间,且不会超过参考值。
公式
2.1 PID 系统定义与公式
r(t) setpoint, reference,是期望的过程值或设定值(SP);
y(t) output, process variable,是测量的过程值,输出值(PV);
e(t) error,是偏差;
u(t) control effort,是控制量;
PID控制器的显着特点是能够利用比例、积分和微分这三个控制项对控制器输出的影响来进行精确和最优的控制。
PID 控制器,不断计算误差值e(t) 作为所需设定点之间的差异SP=r(t) 和测量的过程变量PV=y(t):e(t)=r(t)−y(t) ,并应用基于比例、积分和导数项的修正。
控制器尝试通过调整控制变量来最小化随时间变化的误差u(t)。manipulated variable (MV)。
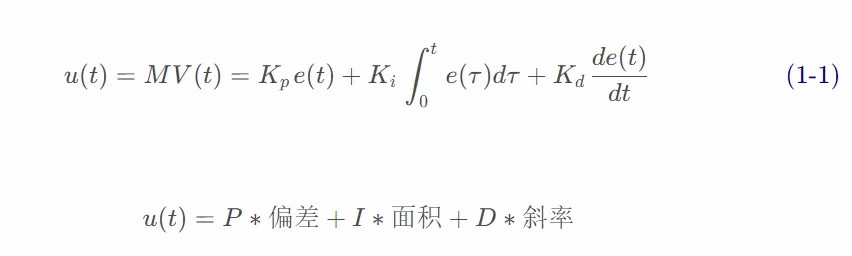

From:
http://matlab.fei.tuke.sk/orhs/subory/podklady/pid_controller_slidy.pdf


2.2 PID 数字公式
由于计算机控制是一种采样控制,它只能根据采样时刻的偏差计算控制量,而不能像模拟控制那样连续输出控制量,进行连续控制。由于这一特点,(式 1-1)中的积分项和微分项不能直接使用,必须进行离散化处理。
离散化处理的方法为:以τ作为采样周期,k作为采样序号,则离散采样时间kτ对应着连续时间t,用矩形法数值积分近似代替积分,用一阶后向差分近似代替微分,可作如下近似变换:

2.3 位置式 PID 算法
将(式 2-1)代入(式 1-1),就可以得到离散的 PID 表达式为
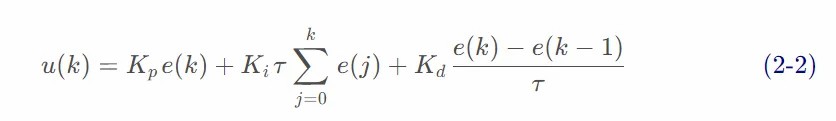
将(式 2-1)代入(式 1-2),就可以得到离散的PID 表达式为
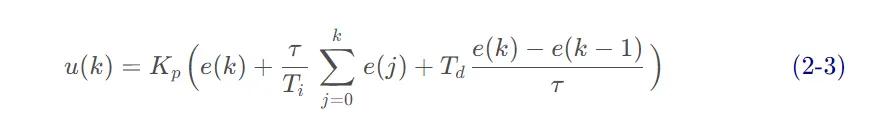
积分系数、微分系数做如下替换:
注意:必须使τ为定值,或者变化小到可以忽略,这样P、I、D才是固定常数,才可能调节
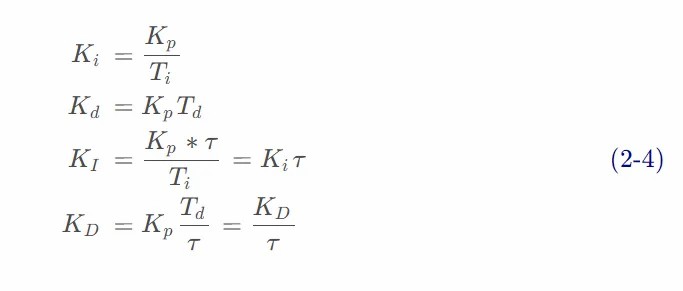

2.4 增量式 PID 算法
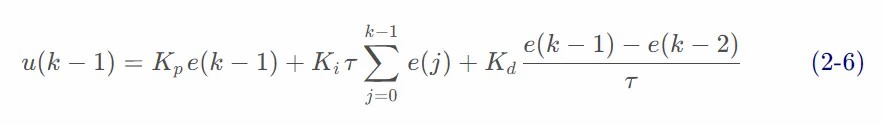
增量式 PID 控制算法可以通过(式 2-2)推导出。由(式 2-2)可以得到控制器的第 k-1 个采样时刻的输出值为:
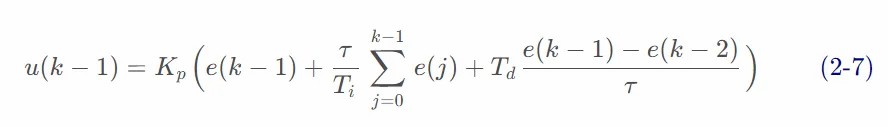
由(式 2-3)可以得到控制器的第 k-1 个采样时刻的输出值为:
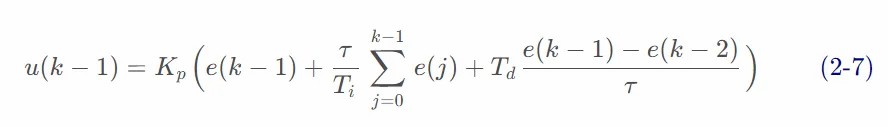
用(式 2-3)减去(式 2-7)相减并整理,就可以得到增量式 PID 控制算法公式:
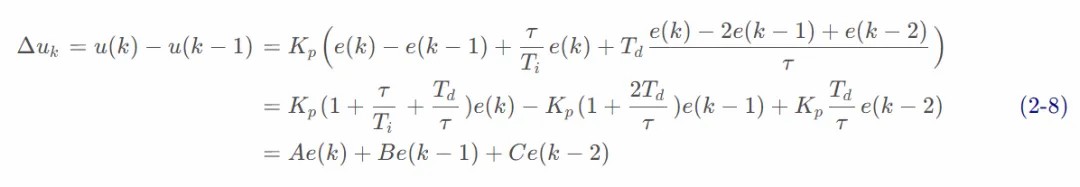
由(式 2-8)可以看出,如果计算机控制系统采用恒定的采样周期τ,一旦确定 A、 B、 C,只要使用前后三次测量的偏差值,就可以由(式 2-8)求出控制量。
增量式 PID 控制算法与位置式 PID 算法(式 2-3)相比,只需要保持当前时刻以前三个时刻的偏差值即可,累计误差较小,计算量小的多,因此在实际中得到广泛的应用。
而位置式 PID 控制算法也可以通过增量式控制算法推出递推计算公式:
(式 2-9)就是目前在计算机控制中广泛应用的数字递推 PID 控制算法。
调试技巧
推荐
-

-

QQ空间
-

新浪微博
-

人人网
-

豆瓣

